© 1999-2023 Jürgen Müller
juergen@e-basteln.de
Since the circuit design is very straightforward, the following sub-sections on Instrument Control and Feedback Loop, Tunneling Current Amplifier, and Piezo Drivers will just give brief circuit descriptions and discuss a few design considerations in more detail. The Miscellaneous section at the end currently just has a few remarks on wiring.
The complete schematics are available in PDF format.
Like the Mechanics page, this page begins with a discussion of what I considered the fundamental design decision: Which parts of the STM should be digital, and which analog?
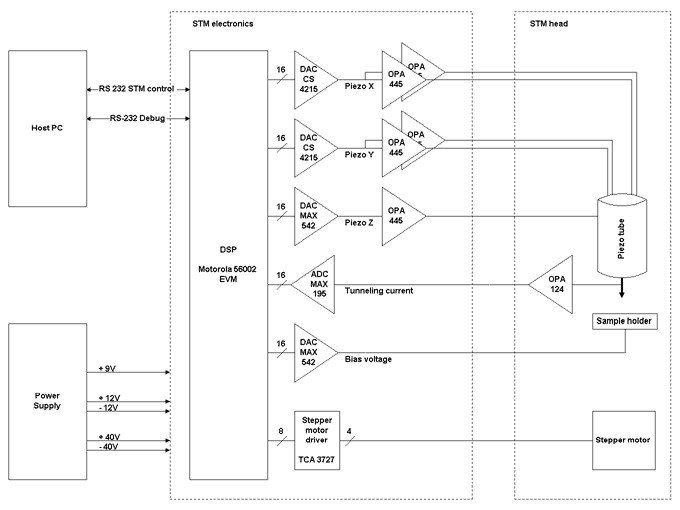
Block diagram of the STM electronics. It is built around a Motorola DSP56002 evaluation board; the DSP controls the X/Y scanning motion as well as the digital feedback loop.
STMs have been built with purely analog electronics - analog sweep generator and Z feedback loop, and an oscilloscope or chart recorder for taking data. I guess this will not be the approach of choice for any STM project today (especially for those of you reading these pages on a computer screen) - a computer looks like the obvious choice, at least for generating the X/Y scans and storing the data. My design considerations quickly narrowed down to two options:
Use the computer for X/Y scanning and data storage only; use an analog feedback loop to keep the tunneling current constant (or a slow feedback loop for constant height scanning with slow drift/tilt compensation).
Build a completely digital system, i.e. control the tip’s X, Y and Z coordinates (plus the bias voltage, if desired) from the computer. Measure the tunneling current via an analog-to-digital converter, and implement a digital feedback loop through the computer.
Some aspects to consider:
Design (1) could be implemented using a standard sound card in a PC; all you would have to build is the analog feedback loop. You would need a decent sound card with real 16 bit resolution and full-duplex capability (playback and recording at the same time). The analog inputs and outputs would probably need to be modified, since they should be DC-coupled; sound cards typically use capacitive coupling. The 44 kHz sampling frequency should be more than sufficient to generate scans and record the Z position. Using the buffered wave recording and playback functions provided in Windows, you could probably get by without any hardware driver programming.
Whether you use sound cards or specialized A/D and D/A converter boards, design (1) offers a nice separation between digital world (inside the PC, typically bought off the shelf) and analog world (outside, home-built). All nasty crosstalk problems caused by high-frequency digital clocks ticking next to sensitive analog circuitry have hopefully been solved by the designer of your PC plug-in board, which may save you some headaches.
Design (2) could probably not be implemented using a sound card! All modern sound cards seem to use sigma-delta converters (or similar concepts?), which feature high resolution and linearity, but also introduce a long delay until the converted signal appears at the other end; 16 sampling cycles for both D/A and A/D conversion appear to be typical for 16 bit converters. This introduces a massive delay into the feedback loop, limiting the bandwidth to very unattractive values. Hence, at least one pair of fast D/A and A/D converter is needed for measuring the tunneling current and controlling the tip’s Z position.
While a PC should certainly have enough processing power to implement design (2), that real-time power is not easily available to a Windows application. Using DOS or some real-time operating system should work - but it would be nice to use Windows to display cool graphics of the scans… A dedicated microprocessor or DSP for the feedback loop is probably the best choice.
Design (2) gives you more flexibility in controlling the tip’s Z position: Switching between constant height and constant current mode, spectroscopy modes that may keep a constant height while varying the gap bias, adaptive feedback for optimized scan speed etc. can all be implemented in software. A safe coarse approach mode can be implemented by repeatedly retreating the tip all the way, making a coarse approach step, slowly expanding the tip while looking for tunneling current etc.
The last aspect finally led me to choose design (2). Since I wanted to use the STM with my laptop computer (which does not have decent - let alone full-duplex DC-coupled - sound), I decided to handle all the analog I/O from the dedicated slave processor. I finally picked a Motorola DSP 56002 evaluation board as the slave processor; some reasons are given in the next section.
The digital control and feedback loop of the STM is built around a Motorola DSP 56002 evaluation board. The 56002 is a fixed-point signal processor, running at up to 66 MHz, with the 24 bit word size preferred by Motorola.
Any other signal processor would probably work as well, as would a decent microprocessor. The processing power is not too critical, from what I have seen so far - a few feedback loop calculations at a 32 kHz sampling rate, and handling the serial port at 115 kBit/s (11.5 kHz maximum interrupt rate). I would not suggest using an 8 bit micro-controller for this task, but even that might work.
My decision for the 56002 was mainly due to the peripherals Motorola put on the evaluation board, and due to software considerations:
Unpleasant update (May 2006): The DSP56002 evaluation board used in this project has been discontinued a few years back, “due to lack of availability of memory components required for this product”. By now, the 56002 processor itself has gone out of production as well. The 563xx DSPs are supposed to be fully backward compatible with the 56k series, but I could not find a suitable evaluation board during a quick check (at least not from Freescale themselves, which is the new home for Motorola’s semiconductor business). You can still find the DSP56002 evaluation kit on ebay – it was popular with radio amateurs, so there seem to be quite a few of these boards around. As of today, Freescale still offer documentation for the 56k products on their website.
As shown in the block diagram above, the DSP56002’s peripherals are
This part of the circuit is somewhat difficult to describe, since I don’t want to include the circuit diagrams for the 56002 evaluation board here, which are Motorola’s property. They come with the evaluation board, and I don’t think they are available on Motorola’s web site, so Motorola might be serious about their copyright. I’ll describe my own add-ons by referring to the circuit diagram (PDF format), and begin with a very short explanation of the interface to the DSP.
All D/A and A/D converters are connected via the 56002’s "Synchronous Serial Interface" (SSI). That’s a serial interface using separate Data In, Data Out, and Clock lines. To allow several devices to share the SSI, full transmission cycles are indicated by a separate "Frame Sync" signal, and can be divided into several time slots. The first device’s time slot begins with the Frame Sync; when the device has completed its transmission, it generates another Time Slot signal for the next device in the chain, etc. The on-board AD/DA codec of Motorola’s 56002 evaluation board (Crystal semiconductor CS4215, a device intended for PC sound cards) supports the full SSI protocol directly, as do many other codecs.
It would be straightforward to add a second CS4215 to the evaluation board to get additional DA and AD channels. But the CS4215 introduces long signal delays - both the AD and DA part have digital, oversampled filters, each causing 16 sampling cycles of delay. Hence, they are not suitable for use inside the digital feedback loop.
The Maxim DA and AD converters I chose (because I got free samples) can handle 85 ksamples/s AD (MAX195) and some 300 ksamples/s DA (MAX542), each at 16 bit resolution, and with no built-in filter delay. They both have serial data transfer with a separate clock, but lack the intelligence of synchronizing themselves to a "Time Slot" start signal. Instead, both need Chip Select signals to be active during the entire data transfer cycle. It’s the task of the 22V10, a Lattice GAL, to generate these signals with a suitable timing. The data transmission cycle is started by the delayed Time Slot signal from the CS4215. The two DA converters are addressed in direct succession, so they can be addressed from the DSP just like a second codec.
If you are really curious, the GAL assembler listing and JEDEC file are here.
Nothing special happens in the rest of the circuit: Separate +/- 5V supplies are generated locally, as well as a buffered 2.5V reference voltage. The cut-off frequencies of the low-pass filters for the DA outputs may need to be changed later. The input filter for the MAX195 is a second-order Bessel low-pass which I found in Tietze-Schenk, a (the?) German electronics handbook. The cut-off frequency can be tuned from approx. 1200 to 12000 Hz via the resistors at the input, while the amplification remains fixed (at about 1.3).
The following section focuses on the amplifier that converts the small tunneling current to a measurable voltage. It starts with a longish theoretical discussion of the circuit I use (which is very simple), and the requirements and limitations I expected to find.
I finally got around to add another section describing experimental results obtained from the amplifier mounted on my STM head. Instead of the Burr-Brown OPA124 operational amplifier I had intended to use, I switched to the OPA627 (also from Burr-Brown), since the OPA124 exhibited some strange, non-linear stability problem at high output voltages. Hence, I also added estimates for the OPA627 in the theoretical section.
The requirements for the current amplifier are simple enough: Convert the small tunneling current to a voltage which can be handled comfortably, and do it as fast as possible to allow for fast Z height tracking and fast scanning.
Amplification: Typical tunneling current setpoints seem to be on the order of 1 nA. To allow flexibility for higher setpoints, and leave some headroom in case the tip comes closer to the sample than desired, tunneling currents of about 100 nA should be handled without overflows. Some applications require tunneling currents as low as a few pA, but that means very high amplification and hence low …
Bandwidth: For a given amplification, only limited bandwidth will be available. While the quantitative estimates are straightforward, I found the results less than obvious or intuitive. Hence, there’s a separate sub-section on Stability below.
Since the tunneling current grows exponentially with a decreasing tip/sample distance, the response of the overall feedback loop should not be simply proportional to the measured current deviation. Many designs include a logarithmic amplifier, to obtain a Uout log (Itunnel). Logarithmic amplifiers are basically op-amps with a diode (which has an exponential I(U) dependence) in the feedback path. Precision log-amps are available, e.g. from Burr-Brown and Analog Devices.
The current amplifier is located on the STM scanning head (right next to the tunneling junction itself), shown in sheet 6 of the circuit diagram. It’s just a single operational amplifier, used in a transimpedance configuration with high amplification: The input is a small current Itunnel, and the output is a voltage Uout = Rfeedback * Itunnel. With Rfeedback = 100 MOhm, a (typical) tunneling current of 1 nA will produce a voltage of 100 mV. I hope the total noise will be below 5 mV, allowing a current resolution of some 50 pA.
The positive input of the op-amp is connected to the bias voltage; the op-amp will maintain a condition where the negative input (the tip) is at the same potential, which establishes the desired bias between the tip and the sample, which is always at ground potential. An offset trimming resistor is shown in the diagram, but I intend to omit it. A small input offset voltage would just shift the bias somewhat; this will probably be negligible, or can be corrected in software.
I decided to try and omit the logarithmic amplifier. It’s not cheap, and it introduces additional complexity into the circuit when you want to use both positive and negative bias voltage and tunneling current: Since the logarithm is defined for positive arguments only, the absolute value of the voltage must be fed to the log-amp. I hope the dynamic range of the tunneling current A/D converter will be large enough, and have implemented the log (abs (I)) operation in software.
I tried to figure out the bandwidth to be expected from the current amplifier before building it, as well as the way to achieve it. Specifically, I was wondering whether the capacitor in parallel to the feedback resistor Rf, which I found in some published STM schematics, was really necessary. (I knew it is in other applications, e.g. monitoring small photodiode currents.) The following discussion follows the lines of Burr-Brown’s application note AB-050, "Compensate transimpedance amplifiers intuitively", which I found very helpful.
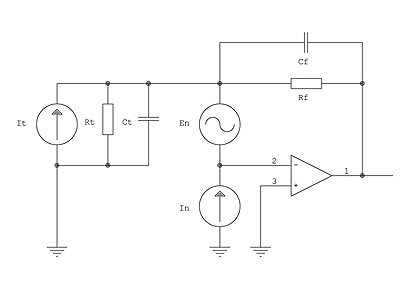
A simplified schematic highlighting the op-amp noise contributions
Consider this simplified diagram. Besides the "real" components in the circuit, noise sources for amplifier current noise inand voltage noise en are shown. The tunneling junction is represented by a perfect current source it, as well as a resistance Rt and capacitance Ct of the tunneling junction and its connection. In typical STM applications, I estimate
Rt = Ubias / Itunnel
= 0.1V / 1 nA = 100 MOhm,
Ct = 10 pF.
The capacity estimate assumes 3 cm of shielded connection wire (2 pF/cm, conservative estimate), 1 pF input capacitance of the op-amp, and some additional stray capacitance. I hope I’m not totally off base there… In the feedback loop,
Rf = 100 MOhm is chosen for suitable amplification,
and
Cf = ?? is to be determined.
To check for stable operation, calculate the noise gain, i.e. the closed-loop amplification for the voltage noise source en shown in the diagram:
Acl(f) = (Rf+Rt)/Rf * (1 + j f/fz) / (1 + j f/fp) with
fz = 1 / [2 π (Rf Rt)/(Rf+Rt)
At high frequencies, the amplification depends on the capacities only, and approaches
Acl(f>>fp) = 1 + Ct/Cf..
Stable operation at optimum bandwidth is achieved when the closed-loop gain at the pole frequency is equal to the open-loop gain of the op-amp, i.e.
Acl (fp) = GBW/fp,
where GBW is the Gain-Bandwidth product. For the OPA124, GBW = 2MHz; the OPA627 has a larger bandwidth at GBW = 16MHz. The solution of the resulting quadratic expression, courtesy of Burr-Brown, is
Cf = 1/(4 π Rf GBW) [1
With the typical numbers give above, we get Cf < 0.1 pF for both op-amp types. This means that very likely no additional feedback capacitance will be needed - 0.1 pF are easily caused by stray capacitance of the resistor leads, circuit board etc. In fact, the main challenge will probably be to keep that stray capacitance as small as possible: Looking back at the expression for fp, we get
fp = 16 kHz for Cf = 0.1 pF, but only
fp = 1.6 kHz for Cf = 1 pF, which might well be more realistic.
A common suggestion is to put the Rf resistor on standoffs to reduce capacitive coupling to the circuit board.
I’ll add more information here as soon as I have practical experience with the circuit!
Noise on the op-amp output is closely related to the stability problem discussed above. In fact, the voltage noise en, amplified by the noise gain Acl(f), will turn out to be one major noise source in typical STM configurations
All calculations will assume a resistor value R = 100 MOhm,
and a bandwidth B = 15 kHz. The three noise contributions
to consider are:
Resistor noise: The feedback resistor itself will produce thermal noise (caused by thermal fluctuations of electrons inside the resistor), no matter how perfect the op-amp. Its contribution is
uresistor, eff = (4 kT R B)1/2,
with Boltzmann’s constant k, absolute temperature T, and resistor value R and bandwidth B. For the example values and T = 300K,
uresistor, eff = 160 µVrms.
Current noise: The shot noise of the amplifier’s input bias current. Since op-amps with very small input bias current are used in the tunneling current amplifier (we want to measure small currents!), this error contribution is small, even after being amplified by the feedback resistor R. Typical current noise density is specified as in = 0.5 fA/Hz1/2 for the OPA124, and in = 2.5 fA/Hz1/2 for the OPA627 (however, the ‘627 spec is for 100Hz frequency, only; I wonder what happens at other frequencies…). This would result in
ucurrent,eff = in R B1/2
= 6 µVrms for the OPA124 or
ucurrent,eff = in R B1/2
= 14 µVrms for the OPA627.
Voltage noise: As discussed above, the amplifier’s input voltage noise will be amplified by the error gain, which depends on the capacitance of tunneling junction and feedback. network. For the OPA124, total input voltage noise is approx. en = 4 µVrms for 15 kHz bandwidth; for the OPA627, it should be around en = 2 µVrms. Assuming Ct = 10pF, Cf = 0.1pF (a conservatively large ratio), this is amplified to
uvoltage, eff = en (1 +Ct/Cf)
= 400 µVrms for the OPA124 or
uvoltage, eff = en (1 +Ct/Cf)
= 200 µVrms for the OPA627.
Short summary and discussion: Current noise is negligible for the low-bias current op-amps typically used in STMs. For the large feedback resistor assumed here, the dominant term may actually be caused by the resistor alone, but op-amp voltage noise may be amplified to comparable values (depending on capacities). The total noise estimate is well below 1mV, corresponding to 10pA of tunneling current, which should be good enough for decent images.
So - how do these estimates hold up in practice? The next section has some real-world results obtained using the OPA627.
The current amplifier I currently use looks exactly as simple as planned - just the OPA627 op-amp with a 100 MOhm feedback resistor. It is mounted on the STM head, directly above the piezo tube, to keep the tip connection short. The capacitors visible in the left picture below are just to bypass the supply voltages; no capacitor is used in the feedback. To shield the high-impedance amplifier from outside noise, an enclosure turned out to be essential. The right picture shows the small case I made from sheet metal (0.1 mm brass).

Current amplifier mounted on STM head, and brass enclosure for amplifier
Bandwidth
Without a feedback capacitor, the frequency response of the OPA627 does show a weak resonance somewhere above 20 kHz, as shown in the diagram below. This was measured by connecting another 100 MOhm resistor to the op-amp’s input as a dummy tunneling junction (plugged into the tip mounting, so the realistic tip connection is in place). Using the AudioTester software, a sinusoidal signal was fed into the op-amp, and the response measured directly at the op-amp’s output (pin 6). In this case, it’s a bit unfortunate that the AudioTester and my soundcard would not let me measure the behaviour at frequencies above 20 kHz.
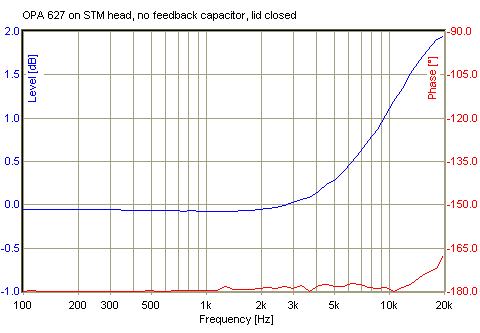
Frequency response of OPA627 mounted on STM head
This looks like a reasonable frequency behaviour. The slight resonance of the current amplifier should be cancelled by the 2nd order lowpass filter located between the amplifier and the A/D converter. I actually tried to measure the frequency response of the complete feedback chain (current amplifier, low-pass, A/D and D/A conversion with software feedback inbetween, and piezo driver). However, the integrating behaviour of the feedback loop (where the change in the output signal is proportional to the input signal) gave me problems in the open feedback loop: Small offset voltages are integrated as well, and cause the output signal to rapidly drift out of range. Also, the mechanical resonance of the STM head and piezo - which will quite likely limit the feedback loop bandwidth - is not included in this type of measurement. I plan to measure the step response in the closed feedback loop, instead, and use that to optimize the loop parameters.
Noise
Since I did not have access to an RMS noise meter, I just estimated the noise at the OPA627 output from the oscilloscope trace. It’s around 4mVrms. Since I don’t really know the actual bandwidth of the amplifier, due to the limited measurement range above, it’s hard to compare this to the theoretical estimates. But one can get more well-defined data one step further down the line:
I included code in the DSP software to monitor the A/D-converted tunneling current signal, and calculate a true RMS value. At that stage, the signal bandwidth has already been limited by the 2nd order lowpass filter. With the filter cutoff frequency set to 8 kHz, the noise is exactly 1 mVrms. That value may go up slightly, since the bandwidth setting is preliminary, but not by more than a factor of 1.4. Hence, I should be able to measure tunneling current with a resolution of 10..15 pA.
While that will hopefully be good enough, there is still some discrepancy compared to the theoretical estimates; about a factor of 3 or 4. I am curious to find out about the reason for this deviation, but not too much so, as long as the amplifier turns out to be sufficient for good STM images…
The basic decision in designing the piezo drivers was the desired maximum voltage, which depends on the desired scan range, of course. As discussed on the Mechanics page, the expected sensitivity of the piezo tube is about 20..30 nm/V in the bending (X/Y) mode, and 5 to 10 nm/V in the longitudinal (Z) mode.
If all you are interested in is atomic resolution, a standard +/- 12 to 15 Volt supply should work fine, giving a scan range of 200 nm or more. Decent regulated power supplies are readily available and inexpensive. (I wouldn’t suggest using a switched supply, like the ones used in personal computers, to avoid noise on the supplies.)
A somewhat larger scan range is still accessible with the same simple design approach: I found inexpensive voltage regulators and op-amps working at supply voltages up to +/- 40V. This should be good for 1..2 µm of lateral scan range when driving opposing piezo segments anti-symmetrically. Power dissipation (i.e. heat) is not yet a problem at this voltage, and the STM does not present a serious shock hazard. Hence, this is the voltage range I finally decided to use.
Initially, I liked the idea of a much larger scan range for work on larger scales; not too many samples are available for atomic-resolution work under ambient conditions. Designing a power supply and linear driver for operating voltages of a few 100 volts seems definitely possible, but the circuit examples I found suggested to me that a fair amount of work and experimentation would have to go into that part of the design alone. (And I would stand a good chance of electrocuting myself in the process…). I concluded that I did not want that hassle.
This description refers to the circuit diagram, which is available in PDF format.
As mentioned before, I built my own power supply, mostly due to the somewhat unusual 40V requirement (circuit diagram sheet 2). The LM317 HVT adjustable regulator is used for both the positive and negative supply voltage. It can handle output voltages from 1.2 to 57V, and it’s short-circuit proof up to 60V input voltage (a capability I have verified more that once). There is a corresponding type for negative voltages, but the LM337 is limited to 40V input / 37V output voltage, which is why I used the positive type for both supplies. Texas Instruments’ TL783 is a similar regulator, for up to 125V output voltage.
The piezo drive circuit itself is very simple (circuit diagram sheet 3). It uses the OPA445 from Burr-Brown, an operational amplifier good for +/- 45V supply voltage, to drive the piezo tube. To get the most scan range out of the available voltage, opposing electrode pairs are driven anti-symmetrically.
By the same token, I also intend to produce Z excursions by driving the inner electrode of the piezo, rather than adding a Z voltage to all outer electrodes. I’m not sure about this idea, though - it might be better to keep the inner electrode at ground, to provide a shield for the tip connection. Hence there are jumpers for routing the Z voltage to the outer electrode drivers and for grounding the inner electrode.
The CA3240 (dual op-amp) input stage level-shifts the scan voltage, which comes from the CS4215 codec on the Motorola evaluation board. Since the codec uses +5V supply only, its analog output is centered around a CMOUT voltage (approx. 2.1V) generated by the codec, rather than around 0V.
The OPA445 is not exactly a power amplifier; output current is limited to 15mA. Is this enough? I tried to estimate this beforehand; the calculations are in the following paragraphs. The result is that the OPA445 should be fine for driving the four outer electrodes in all applications. I’m not absolutely sure about the inner electrode, since I don’t yet know the bandwidth I’ll get from the tunneling current amplifier, which will probably limit the overall feedback loop bandwidth. If the piezo driver turns out to be the limit, I might add booster transistors behind the op-amp.
The OPA445 is available in TO-99 (metal can) and plastic DIP packages. I use the DIP package type, which was more easily available and cheaper. Cooling is achieved mostly via the connecting leads, and my way of mounting the ICs (precision sockets; no large circuit board area connected) is less than ideal. The chips get quite warm, but not uncomfortably hot.
Of course, Burr-Brown also specifies a limit on the total power consumption - 680mW, which means just 8mA per supply at 40V. Not much, considering the 3.8mA quiescent current…
So far, I have measured the total current consumption of all 5 op-amps together, both in "silent" and in scanning mode (scanning X/Y at 50Hz, Z at 100Hz, all with full-scale voltage amplitude of 37.5V, and with 4*10nF dummy loads connected). The result was 20 mA for all 5 op-amps - both in silent and scanning mode. The value agrees well with the specified quiescent current. It seems to make sense that no power is consumed to drive a "perfect" capacitive load (at any time, the sum of currents supplied to the 5 electrodes should cancel), but I’m surprised that the op-amps don’t introduce any measurable losses. Maybe some additional power will be consumed once I connect the piezo tube, which might introduce more dielectric losses than the 4 capacitors used here. Anyway, operation should be safe unless I go to much higher scanning frequencies (which seems unlikely at full voltage range).
Between any pair of electrodes, some capacitance will be present, depending on electrode geometry and the dielectric constant of the ceramic material between the electrodes. The capacity between the inner electrode and any outer electrode is by far the largest.
C = eps eps0 A/h
with electrode area A = π/2 L D, for tube length L and diameter D; tube wall thickness h, vacuum permittivity eps0 = 8.85E-12 F/m, and relative dielectric constant eps = 2750 (for BM527 at 1 kHz; values for other piezo ceramics range from 1000 to 3500).
For my piezo tube L = 25 mm, D = 6.5 mm, h = 0.7 mm, made of BM527, I obtained C = 9 nF. Measurements have since suggested that the actual value might be somewhat smaller, but the order of magnitude seems right.
The op-amp driving the inner electrode will see the 4-fold capacitance. This is only limiting the slew rate of Z excursions - since bending the piezo in X/Y always involves anti-symmetric changes on two outer electrodes, no charge needs to be moved to or from the inner electrode.
Once the capacity C is known, the drive current I necessary to drive the piezo with a sinusoidal voltage of frequency f and amplitude U can be calculated:
I = 2π f U C
For a full-range scanning motion with U = 37V, f = 2kHz and the outer electrode’s capacity C = 10 nF, we get I = 5 mA. (Pretty fast scanning assumed here; if possible at all, this could only be used in constant height operation.)
For faster but smaller Z corrections with U = 2V, f = 20kHz and the inner electrode’s capacity C = 40nF, the result is I = 10mA. (This is still a rather large Z step of more than 1 nm. Since the tunneling current typically changes by an order of magnitude every 0.1 nm, I can’t see how such a large Z correction could happen in a single step in practical feedback operation?)
To verify these estimates, I measured the frequency response of an OPA445 driver stage with the piezo tube connected. Results are shown here for the Z drive (driving the inner electrode, with all outer segments grounded). Red denotes the amplitude, blue the phase:
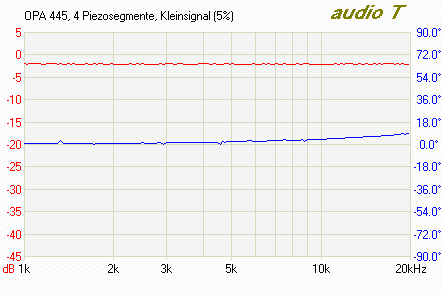
Small signal response of the OPA 445 piezo driver (5% of full voltage range)
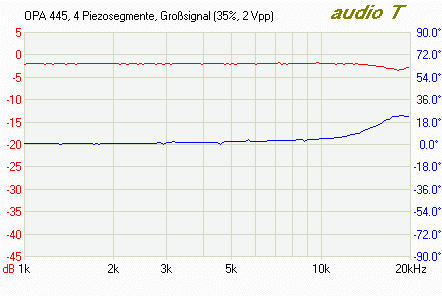
Large signal response of the OPA 445 piezo driver (35% of full voltage range)
The result, as already cited above: The OPA445’s 15mA output current should be plenty for driving the outer electrodes. For the inner electrode, the OPA445 might limit the performance in extreme situations, but I assume the overall speed of the Z feedback loop will be limited by the tunneling current amplifier, rather than the piezo driver.
Two separate metal cases are used to house the power supply and the electronics (both digital and analog). I was worried about magnetic fields from the transformers coupling noise into the circuit - especially the STM head itself. Since magnetic fields are not easily shielded, I just plan to put the power supply some distance away from the electronics and the scanning head.
The electronics are mounted on several separate circuit boards, as shown in the circuit diagrams. I used prototyping boards with individual soldering pads and hand-wired the connections - not beautiful, but probably quite good with regard to crosstalk, since wires don’t run in parallel for longer distances. The boards for the piezo drivers and for the AD/DA converters are double-sided, with a ground plane on the component side.
The DSP board and all analog boards are inside the same metal case; currently with no shielding measures and just with ribbon cable to connect them (a connection style suggested by the numerous 2*x headers on the evaluation board). This might come back to haunt me; I’m half-prepared to use at least some shielded cable, or to try and separate the boards by a grounded plane.
Several papers in the literature stressed the importance of avoiding
ground loops in the circuit, again to avoid inductive coupling
of noise from magnetic fields. Hence separate ground lines for
the different voltages are brought out from the power supply,
and connected only where signals move from the digital to the
12V analog domain, and from the 12V to the 40V circuit. I hope
this will be good enough, and did not use any opto-isolation.
(I might need to add some inductance between digital and analog
grounds to keep the digital noise out.)