© 1999-2023 Jürgen Müller
juergen@e-basteln.de
The mechanical components of an STM should do three things: Bring the tip into tunneling distance from the sample (coarse approach), keep it there in a stable position (undisturbed by vibrations and thermal drifts), and scan it across the sample with sub-nanometer resolution. This page tries to address all relevant topics, beginning at the center of the STM: Piezo element for scanning motion, approach mechanisms and materials for the scanning head, and vibration isolation systems. In most sub-sections, I’ll try to give a brief overview of design options described in the literature, followed by some details of my own implementation.

The STM head on its pendulum-type vibration isolation base. A glass beaker stops air currents and provides some sound-proofing.
Piezo elements are apparently used universally to produce the small motions (on the nanometer scale) of the tip in scanning probe microscopy. Piezoelectric materials - most notably some types of ceramics that have been polarized by letting them cool down in the presence of an electric field - exhibit a mechanical deformation when a voltage is applied across them. The exact amount of deformation depends on the material and its geometry (some more details will follow below); typically, excursions of a few nanometer/Volt may be obtained from handy piezo elements, say 1 inch in length.
Once you know what you want, the piezo scanner may well be the easiest part of the whole STM project: I just bought a piezo tube, complete with the desired electrode configuration, via mail-order; it wasn’t even expensive.
In all designs I have seen, piezos are used both for the X/Y scanning motion and for the Z height tracking. There are, however, a number of different geometries commonly used:
Tripod – the original STM by Binnig and Rohrer, and its early successors, used tripods assembled from three pieces of piezo-electric material, with their polarization (i.e. stretching) axes oriented in three orthogonal directions. Since only the un-amplified stretching motion of the piezos is used, they need to be rather long and thin, making the assembly not as rigid as is desirable.
Tube – a very elegant design, also proposed by Binnig and Smith a few years later (Rev. Sci. Instrum. 57 (8), p. 1688, 1986). A single piezo tube is used, with one electrode on the inside, and for electrode stripes running the length of the tube on the outside. When a voltage is applied between inner electrode and one outer electrode, the material between the electrodes stretches/contracts in the tube’s longitudinal direction. By applying the same voltage to all four outer electrodes, the whole tube can be stretched, for Z tracking. But the tube can also be bent, by applying some voltage to one outer segment only (and optionally the opposite voltage to the opposing electrode segment, for symmetrical deformation). If the tube is mounted on one end, bending will move the other end sideways for the X/Y scanning motion. By far the most common scanner design today; tubes in the described electrode configuration are readily available. Since my design uses a tube scanner as well, some more details follow below.
Bimorphs – "sandwiches" of two layers of piezo-electric material, with electrodes on both sides and an embedded center electrode. Like the tube in bending mode, they bend sideways when a voltage is applied, since one side stretches while the other contracts. Their main advantage seems to be their large excursion per applied voltage (or, put another way, you can keep them short and sturdy to obtain a given excursion, resulting in high resonance frequencies). To me, they lack the elegance of the tube design; you still need to combine multiple bimorphs for 3-axis scanning. Not very common, as far as I can tell.
Unimorph Disk – a design I only learned about when my own STM was largely finished; otherwise I would have been tempted to use it. Similar to the tube design, it uses a single piezo element with multiple electrodes to obtain both X/Y scanning and Z height tracking: A flat disk of piezo material carries a common electrode on one side and 4 segments on the opposing side. The tip is mounted on a post, which translates the warping of the piezo plate into lateral motion. John Alexander, the inventor of the disk scanner, has just published an amateur design using a modified $2 piezo buzzer as the scanner.
A variety of piezo-electric ceramics is available, which differ in their electrical, piezoelectric and mechanical properties. The following table lists just a small selection of properties, as published in the manufacturer’s data sheets, for four types of piezo ceramics commonly used in scanning probe microscopes. PZT-4 is a "hard" piezo ceramic used for power transducers, included for comparison.
Please refer to the manufacturers' web sites for more details. PZT-5A and PZT-5H are frequently mentioned in the literature and are supplied by Staveley Sensors and [Morgan Electro Ceramics]( http://www.morganelectroceramics.com>, among others. BM500 and BM527 are similar materials available from Sensor Technology Ltd., who also have a very helpful brochure, "Piezoelectric ceramics - product catalogue and application notes". A short discussion of the parameters shown follows below.
| Material | PZT-5A | BM500 | PZT-5H | BM527 | PZT-4 | unit |
|---|---|---|---|---|---|---|
| Dielectric constant ε | 1900 | 1750 | 3300 | 2750 | 1335 | — |
| Dissipation factor | 2.0 | 1.6 | 2.0 | 2.0 | 0.2 | % |
| Piezoelectric coefficient d31 | -0.18 | -0.16 | -0.27 | -0.25 | -0.12 | 10-9C/N = nm/V |
| Frequency constant N3 | 1980 | 1800 | 1945 | 1850 | 2250 | Hz m |
| Mechanical quality factor Q | 85 | 80 | 70 | 70 | 500 | — |
| Curie temperature TC | 365 | 360 | 195 | 225 | 325 | deg C |
| Young’s modulus Y | 6.6 | 6.5 | 6.1 | 6.9 | 7.7 | 1010 N/m2 |
| Density rho | 7.9 | 7.7 | 7.6 | 7.5 | 8.1 | g/cm3 |
Values quoted are from Morgan Electro Ceramics' and Sensor Technology’s product literature. All values refer to room temperature, 20°C. Standard tolerances on these values are +/- 20%, according to Morgan Electro Ceramics.
A large piezoelectric coefficient d31 means you get large excursion per applied voltage, which is usually desirable. Large dielectric constants are undesirable, since they mean a large capacitance of the piezo tube, which will limit the scanning frequency obtainable for a given drive current.
Young’s modulus Y and the density rho of the material will influence the resonance frequency. Large Y and small density are desirable for a high resonance frequency (see below), but variations between suitable materials are small anyway.
The Curie temperature is shown to point out that soldering connections to the piezo’s electrodes may require some care: The piezo will lose its polarization, i.e. its piezo-electric property, when heated above the Curie temperature. A high dissipation factor and small quality factor Q mean that a large part of the driving energy is converted to heat inside the piezo. All materials commonly used in scanning probe microscopes are "soft" piezo-ceramics, optimized for high sensitivity (large d31), but with rather large losses. They must not be driven with large amplitudes and at high frequencies, which could heat them up significantly – even beyond the Curie point. See the "hard", high-power PZT-4 data for comparison.
Soft piezo ceramics will also exhibit a larger hysteresis. Sensor Technology mentions 15% to 20% as typical for soft materials, as opposed to 3% to 5% for hard materials.
Considering the 20% tolerances, there’s no massive difference between the soft materials. I decided to go for the somewhat larger scan range (d31) of PZT-5H or BM527, respectively. Since Sensor Technology had the best price (and they were very helpful as well!), I’m now using their BM527 piezo tube.
A few formulas for electrical and mechanical properties of piezo tubes are compiled in this paragraph. Definitions used (and values for the BM527 tube I use in brackets):
L tube length (25.4 mm = 1"),
D and diameter (6.5 mm = ¼ "),
h tube wall thickness (0.7 mm).
I compared the results for displacement responses and resonance frequencies to the experimental values Binnig and Smith obtained on their first tube scanner. Their experimental values were about 25% below the theoretical predictions, both for displacements and resonance frequencies; so the theory is slightly optimistic. I don’t have numbers for my own scanner yet.
C = eps eps0 A/h
with electrode area A = Pi/2 L D, vacuum permittivity eps0 = 8.85E-12 F/m, and relative dielectric constant as given in the table. For my piezo tube, I obtained C = 9 nF. Measurements have since suggested that the actual value might be somewhat smaller, but the order of magnitude seems right. See the Electronics page for a discussion of the effect of the capacity on the driving circuit.
dz/U = L/h d31
gives the ratio of displacement dz per applied voltage U, with the piezoelectric coefficient d31from the table above. For my tube, dz/U = 9 nm/V is expected.
dx/U = 23/2/Pi L2/(Dh) d31
gives the ratio of displacement dx per applied voltage U, with the piezoelectric coefficient d31 from the table above. Anti-symmetric driving of the pair of opposing electrodes is assumed here, causing the tube to bend because it stretches along one side, and contracts along the other. Divide by 2 for the simpler case of driving just one electrode. For my tube, dx/U = 30 nm/V is expected.
fz = (Y/rho)1/2 / 4L
is the resonance frequency in the stretching mode. It depends on Young’s modulus Y and the density rho, which are material constants, as well as on the tube length. The predicted resonance frequency for a BM527 tube and the dimensions given above is fz = 30 kHz.
fx = 0.56 (Y/rho)1/2 [D2 + (D-h)2]1/2 / [8L2]
is the resonance frequency in the bending mode. The dependence on tube geometry is more complicated here. The predicted resonance frequency for a BM527 tube and the dimensions give above is fx= 3 kHz.
The "louse" of Binnig and Rohrer’s first STM (G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel, Phys. Rev. Lett. 49, p. 57, 1982) is an example of what I call "piezo-stepping" devices. It could produce a discrete step by clamping its rear leg to the support surface, expanding the piezo body, clamping the front leg to the surface and releasing the rear leg, contracting the body etc. Clamping was achieved by electro-static attraction; being a three-leg device on a flat surface, the "louse" could actually move in two dimensions. Burleigh Instrument’s commercial "Inchworm" is another, one-dimensional, implementation of a similar concept. It uses a piezo tube sliding on a precision rod.
While these piezo-steppers can provide nanometer steps over a macroscopic range of travel, they appear to be quite unfashionable in more recent designs. My guess is that the separate clamping and moving actuators make them too complicated and expensive, especially compared to the inertial sliders discussed below.
The next generation of STM designs relied heavily on rather straightforward, mechanical approach mechanisms: Just use a precision screw, which is good for micrometer-resolution, and reduce the movement by a mechanical lever or such. The most popular ways of obtaining the necessary reduction are differential springs and mechanical levers. Differential springs consist of a soft spring, which is compressed by a screw, and in turn pushes against a very strong spring supporting either the sample or the tip. Movement is reduced by the ratio of the spring constants, which can easily be 100 to 1000. Mechanical levers are even easier. My favorite design is the tripod, which is shown below in some more detail, since it’s what I chose for my STM.
In most designs, the precision screw is driven by a stepper motor to eliminate the tedium of a manual approach (and the vibrations introduced by touching the instrument). Since the travel of the original precision screw is typically limited to a few millimeters, the range of fine approach is just a few tens of microns. This means that an additional coarse approach mechanism, still of reasonable precision, is needed. Coarse approach is usually done manually, under visual control using an optical microscope. (Since STM sample surfaces are very smooth, a reflection of the tip can be seen on the surface, approaching the tip.)
Inertial sliders appear to be the current fashion in STM design. They are similar to the "piezo-steppers" in that they produce a series of discrete steps, each using one full expansion of a piezo drive. Instead of requiring separate clamping means, they rely on the "tablecloth trick" of slip-stick motion: A translation stage riding on a smooth support, which can be accelerated using a piezo actuator. Due to friction, the stage will follow accelerations up to a certain limit. If the motion is suddenly reversed (by reversing the piezo voltage as quickly as possible), the translation stage will not follow the reverse movement. Perhaps the simplest implementation of the idea is to move the tip wire itself inside a short holding tube, by contracting and expanding the scanning piezo. This design, suggested by Kleindiek and Herrmann, achieves coarse approach without any extra driving element. Papers by Pohl also discuss theory and implementation of inertial sliders.
The two main requirements for materials used for the STM’s base are
The thermal expansion coefficient should be matched to the piezo’s. This prevents large drifts of the tunneling gap width when the instrument’s temperature changes (due to drifts in the environmental temperature, or internal heating of the instrument).
The base should be mechanically rigid, with high resonance frequency. As discussed for the piezo tube itself, the resonance frequency depends on Young’s modulus Y and the density (specific gravity) rho of the material. (And on the geometry of the assembly, of course).
The following table lists typical values for some materials:
| Material | Thermal expansion coefficient k |
Young’s modulus Y | Density rho | (Y/rho)1⁄2 |
|---|---|---|---|---|
| 10-6/K | 1010 N/m² | g/cm³ | m/s | |
| Piezo ceramics | 7.5 (?) | 6.9 | 7.5 | 3000 |
| Macor | 7.4 | 6.7 | 2.5 | 5200 |
| Glass | 5 .. 10 | 6 .. 8 | 2.3 | 5500 |
| Stainless steel | 14.4 | 19.3 | 8.0 | 4900 |
| Brass | 18.9 | 10.3 | 8.5 | 3500 |
| Aluminum | 25.0 | 7.2 | 2.7 | 5200 |
| Acrylic, cast | 70 | 0.28 (?) | 1.2 | 1500 |
| Acrylic, extruded | 80 .. 150 | 0.31 (?) | 1.2 | 1600 |
Macor, a machinable ceramic made by Corning Glass, is apparently the ideal material. Its thermal expansion is closely matched to the piezo ceramic itself, it is very stiff and lightweight, and it is a very good isolator. It is widely used in STMs built in research environments. Macor can be drilled, turned and milled, but with some care - most machine shops will probably not have any experience with the material. Simple designs, requiring just a few holes to be drilled in a pre-cut block, might be suitable for homemade STMs. In Germany, RS Components sells Macor in small pieces and trial packs.
Glass is pretty good as well. In fact, some early STMs were mounted in a glass rod frame. You probably don’t want to machine glass parts, but finding a suitable piece and using it as a base or tip holder might be a viable solution. The data given above are for Pyrex glass (made by Schott); other types of glass may have somewhat larger thermal expansion.
Metals are not really ideal, but can be machined with reasonable ease. Steel is the best choice with regard to thermal expansion and rigidity (but hardest to machine, of course). Between brass and aluminum, there is a trade-off between thermal drift and resonance frequency; both are easily machined.
Acrylic is included beacause it is the best isolator I could come up with that’s easily machinable. Thermal expansion is huge compared to ceramics or even metals; I’m not sure whether the Young’s modulus in the table is correct. Extruded acrylic (most rods, tubes and thin sheets) is even worse than the cast variety (available in blocks or thick sheets).
As mentioned above, I opted for a mechanical tripod for the coarse approach. This design is apparently still quite popular; among many other STMs, it’s used in Digital Instruments' NanoScope, probably the best-selling commercial family of instruments. I got the idea from the paper of Drake, Hansma et. al, but adapted their design to move all components into the head itself. (So I can use the head on any stable base; maybe on an inverted optical microscope in the future.)
The mechanical set-up is simple enough: Both the head and the base consist of single blocks. The head rests on three supports, which are the ball-shaped tips of precision screws. The piezo tube is mounted in the head (glued into the red acrylic block). The sample is attached to the base, via a permanent magnet which is not shown.
The two precision screws in front, next to the piezo tube, have knurled knobs for manual operation. Turning these screws will change the tip - sample distance by nearly the same distance that the screw was moved. Motion of the third support screw in the back, however, is reduced by a factor of about 11: Since the piezo tip is quite close to the line connecting the other two supports, the whole head acts as a lever with ratio 40mm / 3.5mm. This allows for a fine approach using the third screw. For automated approach it is driven by a stepper motor, as described below.
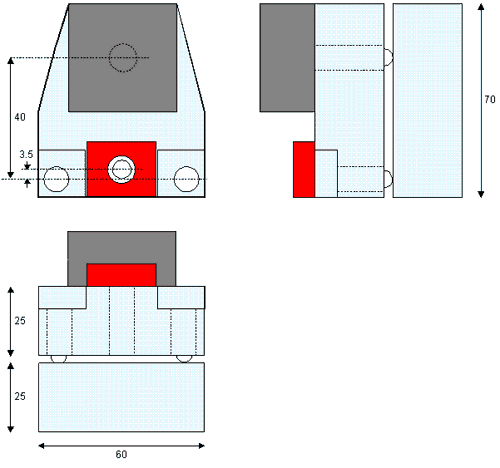
Homebrew STM design. Top view (upper left) and two side views. Bright blue: brass head and base; red: acrylic support for piezo tube; dark gray: stepper motor. All dimensions are in mm.
New! Several readers have asked about more detailed mechanical drawings. Unfortunately, all I have are these scans of pencil drawings (PDF), with handwritten comments in German. Maybe they help; otherwise, please ask or ignore…
The stepper motor is operated in half-step mode, with 400 half steps per revolution. I found that the motor will stand on both the full and half-step positions when it is powered down, so I can turn the chopped motor supply current off while taking scans.
The precision screws are 80 pitch (80 turns/inch), which means about 320 µm/revolution or 0.8 µm/half-step. The motion of the tunneling tip is further reduced by the lever by a factor of 40/3.5, resulting in an average half-step size of 70 nm. I expect significant fluctuations of the step size, due to imperfect screws and support surface, but since the step size is a comfortably small fraction of the expected piezo Z range (9 nm/V * 75V), that should be non-critical.
Total travel of the screw is about 4 mm, which is reduced to 0.35 mm at the tip. It should be easy to bring the tip into that range using the manual coarse approach screws. I plan to use a small pocket microscope (magnification 30x) to observe the tip-sample distance during manual alignment.
Brass is used for most of the base, and cast acrylic for the piezo tube’s top and bottom plate. As discussed above, this is definitely a compromise with regard to thermal stability. I was limited to materials that were reasonably easy to work with. This meant brass or aluminum for the base, and some isolator to mount the tube and the scanning tip. Thermal drift may well turn out to be a significant problem, but I hope for the best.
Considering the schematic diagram below, the acrylic tube holder should not contribute to thermal drift of the tunneling gap at all. The small acrylic tip holder will contribute, but should actually compensate some of the extra expansion caused by the brass base. When the whole STM temperature changes by the same amount, the mismatch between brass and piezo ceramic (over the large distance of 25 mm) dominates. In practice, I expect the piezo tube (and the attached tip holder) to warm up more than the base, due to dissipated scanning energy, so things may actually look somewhat better.
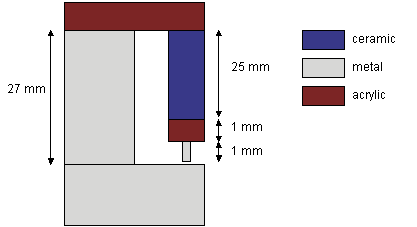
Expected thermal expansion mismatch in my STM:
drift = 27 mm * kbrass - 25 mm * kpiezo
- 1 mm * kacrylic - 1 mm * kbrass
= 250 nm/K.
This design is definitely not for use in cryo-STMs, but it seems to work fine under ambient conditions: I find that the tip remains in tunneling distance from the sample for typically 10 to 20 minutes in a normal room, with the central heating turned on and without special temperature control measures. This should be enough for a series of images. The thermal drift might be noticeable as an artificial slope in the images, but it should be possible to correct for that effect by image processing.
There are a number of very detailed papers on vibration isolation for STMs, and have little experience of my own yet, so I’ll keep this section short. Recommended reading includes the papers by Park and Quate, by Pohl, and by Kuk and Silverman cited in the reference section.
The basic idea is to make the internal resonance frequencies of the STM very high, and to mount it on a support with a very low resonance frequency. The support will follow only the low-frequency building vibrations and suppress most of the high-frequency components. The STM in turn will not be disturbed by the remaining low-frequency vibrations, because they do not introduce any internal motions into the STM (it just moves as a whole).
Typical frequencies are:
1 Hz building vibrations due to people walking around etc.
10..100 Hz building vibrations due to ventilation, appliances etc.
1..10 kHz lowest internal resonance of typical STMs.
The necessary quality of vibration isolation depends, of course, on the amount and spectral distribution of building vibrations present and on the lowest resonance frequency of the STM. As a very coarse rule of thumb, a factor of 1000 between the STM’s and the vibration isolation system’s resonance frequency should be on the safe side. In this case, resonant motions of the vibration isolation platform will be reduced by a factor of 1000² when they reach the tunneling gap. For typical building vibration amplitudes of 1µm, only 1pm = 1/100 Angstrom of excitation amplitude should remain. (But the vibration isloation system will amplify excitations close to its resonance frequency!)
Popular vibration isolation systems used for STMs are
Air support tables: Heavy plate resting on inflated supports, possibly with active regulation to maintain constant height. Nice because they give a large, steady work surface, but expensive and bulky.
"Pendulum": Massive blocks suspended by springs, rubber bands, elastic tubing… Cheap and simple to build. It’s easy to achieve very low resonance frequencies by combining a large mass with a soft suspension; see below for the simple formula. May need some damping to avoid oscillations at resonance - either internal friction of the suspension, or eddy current damping have been used.
Plate and rubber stacks: Have been successfully used with the modern, compact STM designs, which will tolerate some low-frequency vibration. A stack of steel plates (typically postcard-sized and about 1 cm thick), with Viton O-rings or similar rubbery material in between. Since the elastic material is quite stiff, the resonance frequencies of the individual stages are quite high. However, the stack of multiple damping stages (each with different resonance frequency, since the supported mass decreases from bottom to top) is quite efficient.
The papers mentioned above offer excellent theoretical treatments of the different approaches to vibration isolation. Since I plan to use a "pendulum" support, I’ll just recite the simple formulas for that one:
If a block of mass m is suspended by a spring (rubber band…) of spring constant k and length L, the resonance frequency for vertical motion will be
fvertical = 1/(2 Pi) Sqrt (k/m)
and the resonance frequency for lateral motion
flateral = 1/(2Pi) Sqrt (g/L),
where g is the gravitational acceleration, g = 9.81m/s².
Since I don’t have a good feel for estimating spring constants, I find the following relation helpful: If you attach your mass m to the suspending spring, the spring will lengthen by a distance d = g m/k. This can be substituted into the first equation above to give
fvertical = 1/(2Pi) Sqrt (g/d) = 0.5 / Sqrt (d * s²/m).
So the oscillation frequency can simply be estimated from the distance your support spring stretches when you attach the load. An extension under load of 25 cm will result in a resonance frequency of 1 Hz. This can, of course, be achieved by combining a huge mass with a strong spring, or a smaller mass with a soft spring. Results should really be the same, as long as the mass you use (to support the STM) is itself a rigid block, with high internal resonance frequencies.
The lateral resonance frequency will automatically be lower than the vertical one, since L > d is always true once the mass is attached. So it looks like one can’t go wrong here.
I’m currently using a small “pendulum” vibration isolation base - see the picture at the top of this page. A small slab of stone (20204 cm³, 3.5 kg) is suspended from the ceiling above my desk, using three rubber cords. It supports just the STM head; the control electronics sit right next to it on the desk. No dedicated oscillation damping is provided, but the ribbon cable connecting the STM head, plus internal friction in the rubber cords, probably serve that purpose. The picture to the right shows a close-up of the multi-strand rubber cord and the quick-fastener I use for easy length adjustment.
The STM head is covered by a glass beaker during operation. This helps against air currents, but acoustic waves are hardly damped, sometimes even amplified. I’ll try an additional layer of foam or similar material, although the problem does not appear too grave unless you like to sing while taking STM images…
The total weight of stone, STM head and beaker is 5.5 kg. The rubber strands stretch about 45 cm under this load, and as expected the resonance frequency for vertical oscillations is about 0.7 Hz.

The rubber cord stretches somewhat over time. A quick fastener allows for simple height adjustment.
The arrangement seems to work fine (although the final proof will be in taking scans with atomic resolution). However, there were a few quirks I came across when settings things up:
Be sure to attach the rubber cords above the center of gravity of the whole arrangement! I initially guided the rubber cords directly through holes in the stone slab, but found that the additional mass of STM head and beaker moved the center of gravity above the stone’s surface. I’m using rigid hooks now, which extend a few centimeters above the surface, and tied the strings to those.
The rubber cords I got slowly keep stretching while under load. (About 1 cm/hour initially, slowing down over time.) Other materials, especially metal springs, might work better. I don’t find the effect too annoying, since I’m using quick-fasteners at the cords' ends which are easy to re-adjust if necessary.
I noticed a type of oscillation in this mount that was not mentioned in any of the papers I had read: The slab can perform a "nodding" motion, with one string contracting and the opposite one expanding. I expect this problem to be more pronounced for small supports like the one I use: Since it’s a rotation around the slab’s center of gravity, the frequency probably depends inversely on the moment of inertia, which grows rapidly when one moves to larger slabs. - The oscillation frequency is about 2 Hz in my system, and my STM head is significantly more sensitive to it than to vertical motion. But the effect on the tunneling junction has only been obvious when I accidentally touched one of the cords during operation.